第 11 章
変量分析セクション($$v):回帰分析($r)
回帰分析($r)一覧
計算処理型:回帰分析パラメータ
推定値変量作成型:回帰分析パラメータ
回帰係数変量作成型:回帰分析パラメータ
プリント型:回帰分析パラメータ
書式($r in $$v)例1
書式($r in $$v)例1の出力結果
変量記号割当($a)コマンドや変数変換($t)コマンドによって,変量記号の割り当てられている諸変数だけではなく,第7章で述べている演算式をも対象に,回帰分析を行うことができる.ラグ付き変量や対数を含むような回帰分析が1行の式で記述できるのである.また,回帰係数ベクトルの新変量の作成も可能である.関連データをプリントする機能もある.
この章では,回帰分析の諸機能について説明する.
本ページの書式例参照プログラムはWeb版xcampusの場合は各大学のWeb版のプログラム事例として収録され,クリック1つですぐに実行できる.Windows版の場合は,xcampusの[ファイル]メニューの[開く]をクリックして,xcampusの見本プログラム群の[rffmtprg]フォルダに収録されている.UNIX版xcampusの場合は,コマンド xccp を入力することによってプログラム一覧が表示される.
回帰分析には1形式のコマンドと,それを具体化する4形式のパラメータが用意されている.
【コマンド】
回帰分析(regression)コマンドは次の形式をとる.
回帰分析のパラメータは,上述の「$r」コマンドに続いて,4タイプの形式で記述する.個々のパラメータ形式の詳細については,それぞれの項目を参照されたい.演算式そのものについては第7章の後半に説明している.
回帰分析パラメータ一覧
| |
回帰パラメータ形式 |
内 容 |
| 1 |
計算処理型 |
△,run,演算式=(演算式,演算式,…)
<例> △,run,y=(x)
△,run,v=(x,y,z)
△,run,logv=(logx,logy,logz)
△,run,c=(c1,y) |
| 2 |
推定値変量作成型 |
□,■■■,演算式=(演算式,演算式,…)
<例> q,est,v=(x,y,z)
Q,ext,logv=(logx,logy,logz)
r,res,c=(c1,y) |
| 3 |
回帰係数変量作成型 |
□,@■■,演算式=(演算式,演算式,…)
<例> a,@"*,y=(x)
H,@"*,logv=(logx,logy,logz) |
| 4 |
プリント型 |
△,pr■,演算式,演算式,演算式,…
<例> △,pr*,x,y,abs(y-e)/absy)
△,prt,M,m,e/p,f2/q2+18.5 |
但し,□は変量記号,△はスペース,■は特定オペランドの各1文字分である.
書式($r in $$v)例1
書式($r in $$v)例1の出力結果
回帰式のプリント
回帰推定値のプロット
3次元図上の回帰平面
1゜
2゜
- [説明]
このパラメータでは,回帰分析を行って,その計算結果をXCEDIT[XC結果メニュー]の[数値リスト]に出力する.推定値変量の作成などは行わない.
例えば,時系列 y の3期のタイムラグ変量,および r
変量の前期比変化率の2変数を説明変数に,K変量とL変量の比を被説明変数とする回帰分析は,次式で計算処理がなされる.
△,run,K/L=(y3,(r-r1)/r*100)
演算式が変量記号のみの一般的な場合には,回帰処理は次式のように記述することになる.
△,run,z=(x,y,d)
- 1゜ 被説明変数の演算式
被説明(従属)変数を第7章の演算式の構成要素に基づいて記述する.演算式は,変量記号,ラグ付変量記号,定数,関数(対数,指数,絶対値),算術演算子,丸括弧,符号で表記される.ただし,定数のみの演算式は除く.
- 2゜ 説明変数の演算式
説明(独立)変数を第7章の演算式の構成要素に基づいて記述する.
複数の説明(独立)変数による重回帰のばあいは,それらの演算式を「,」で区切って複数個並べることになる.
演算式は,変量記号,ラグ付変量記号,定数,関数(対数,指数,絶対値),算術演算子,丸括弧,符号で表記される.ただし,定数のみの演算式は除く.
1゜
2゜ 3゜ 4゜
- [説明]
このパラメータでは,回帰分析を行って,その計算結果をXCEDIT[XC結果メニュー]の[数値リスト]に出力するとともに,推定値,外挿値,残差などの新変量を作成する.
例えば,時系列 y の3期のタイムラグ変量,および r
変量の前期比変化率の2変数を説明変数に,K変量とL変量の比を被説明変数とする回帰分析で,K/Lの比率の推定値を新変量
k とする処理は次式でなされる.
k,est,K/L=(y3,(r-r1)/r*100)
演算式が変量記号のみの一般的な場合で,推定値や残差の新変量を作成するには次のように記述する.
f,est,z=(x,y,d)
r,res,z=(x,y,d)
- 1゜ 新変量の変量記号 任意の英字1文字,または「?」記号つきの任意の英字1文字
変量に与えるべき変量記号を指示する.任意の小文字,大文字の英字1文字,「?」記号のついた英字の大文字,小文字が使用できる.つまり,a,b,…,z,A,B,…,Z,?a,?b,…,?z,?A,?B,…,?Zのいずれかを記述する.
但し,これまでに割り当てられた変量記号も含めて,すべての変量記号は互いに異なっていなければならない.既に別の変量に割り当てられている変量記号と同じ記号を新変量に割り当てることもできるが,そのばあいには前の変量への割当は解除され,新変量への割当のみが存続することになる.割り当てられた変量記号は当該セクションだけではなく,これ以降の別のセクション内においても有効である.
この但し書きは,新変量の変量記号すべてに共通することである.それゆえ,以下の各パラメータでは但し書きの記述を省略している.
- 2゜ 推定値オペランド
特定の3文字
- 「est」
3゜の被説明変数と4゜の説明変数のすべての変数に数値の入っているケースだけを対象に回帰分析を行い,その共通項のケースに対して被説明変数の推定値(estimate)を求める.
- 「ext」
3゜の被説明変数と4゜の説明変数のすべての変数に数値の入っているケースだけを対象に回帰分析を行い,その被説明変数の推定値を求める.説明変数の数値の入っているデータ期間(ケース範囲)が被説明変数のそれよりも長いばあい,外挿(extrapolation)による推定値が得られる.
- 「res」
3゜の被説明変数と4゜の説明変数のすべての変数に数値の入っているケースだけを対象に回帰分析を行い,その被説明変数の実績値から推定値を差引いた残差(residuual)を求める.
- 3゜ 被説明変数の演算式
被説明(従属)変数を第7章の演算式の構成要素に基づいて記述する.演算式は,変量記号,ラグ付変量記号,定数,関数(対数,指数,絶対値),算術演算子,丸括弧,符号で表記される.ただし,定数のみの演算式は除く.
- 4゜ 説明変数の演算式
説明(独立)変数を第7章の演算式の構成要素に基づいて記述する.
複数の説明(独立)変数による重回帰のばあいは,それらの演算式を「,」で区切って複数個並べることになる.
演算式は,変量記号,ラグ付変量記号,定数,関数(対数,指数,絶対値),算術演算子,丸括弧,符号で表記される.ただし,定数のみの演算式は除く.
1゜
2゜ 3゜ 4゜
- [説明]
このパラメータでは,回帰分析を行い,その回帰係数の推定値ベクトル変量ないしは回帰係数推定値のスカラー変量を新規に作成する.
例えば,時系列 y の3期のタイムラグ変量,および r
変量の前期比変化率の2変数を説明変数に,K変量とL変量の比を被説明変数とする回帰分析で,回帰係数推定値ベクトルの新変量
F を作成するばあい,次式のように記述する.
F,@"*,K/L=(y3,(r-r1)/r*100)
演算式が変量記号のみの一般的な場合で,回帰係数推定値ベクトルの新変量Hを作成する記述例は次のようになる.ベクトルHの第1要素は,1番目の変数xの係数推定値,第2要素は,2番目の変数yの係数推定値,第3要素は,3番目の変数dの係数推定値,第4要素に定数項推定値が入る.
H,@"*,z=(x,y,d)
- 1゜ 新変量の変量記号 任意の英字1文字,または「?」記号つきの任意の英字1文字
変量に与えるべき変量記号を指示する.任意の小文字,大文字の英字1文字,「?」記号のついた英字の大文字,小文字が使用できる.つまり,a,b,…,z,A,B,…,Z,?a,?b,…,?z,?A,?B,…,?Zのいずれかを記述する.
- 2゜ 回帰係数推定オペランド
特定の3文字
- 「@”*」
回帰分析を行い,その回帰係数の推定値ベクトルを作成する.ベクトルの第1要素に1番目の説明変数の回帰係数推定値,第2要素に2番目の説明変数の回帰係数推定値,……,最後の要素に定数項の推定値が入る.回帰分析の計算結果も併せて出力する.
- 「@”.」
回帰係数の推定値ベクトルを上のオペランドと同様に作成するが,回帰分析の計算結果は出力しない.
- 「@00」
回帰分析を行い,その定数項の推定値のスカラー変量を作成する.
- 「@01」
回帰分析を行い,その1番目の説明変数の回帰係数推定値のスカラー変量を作成する.
- 「@02」
回帰分析を行い,その2番目の説明変数の回帰係数推定値のスカラー変量を作成する.
- 「@03」
回帰分析を行い,その3番目の説明変数の回帰係数推定値のスカラー変量を作成する.
- : 以下,同様.
- 3゜ 被説明変数の演算式
被説明(従属)変数を第7章の演算式の構成要素に基づいて記述する.演算式は,変量記号,ラグ付変量記号,定数,関数(対数,指数,絶対値),算術演算子,丸括弧,符号で表記される.ただし,定数のみの演算式は除く.
- 4゜ 説明変数の演算式
説明(独立)変数を第7章の演算式の構成要素に基づいて記述する.
複数の説明(独立)変数による重回帰のばあいは,それらの演算式を「,」で区切って複数個並べることになる.
演算式は,変量記号,ラグ付変量記号,定数,関数(対数,指数,絶対値),算術演算子,丸括弧,符号で表記される.ただし,定数のみの演算式は除く.
1゜ 2゜
- [説明]
このパラメータでは,2゜の各演算式のデータ・プリントを行う.データ・プリントは,従来はプリント($p)コマンドによる方法が一般的であったが,Windows95/NT版では変数変換($t)や本章の回帰分析($r)における「pr*」オペランド,「prt」オペランドが主として用いられる.表計算への出力において最大32列(変量)の一括出力が可能である点や,演算式が利用できる点で優れている.企業名については最大4変量(半角16文字)までが1列にまとめられて出力される.
例えば,時系列 y の3期のタイムラグ変量,および r
変量の前期比変化率の2変数を説明変数に,y
変量を被説明変数とする回帰分析で,推定値の新変量 Y ,推定値 Y
の観測値 y
に対する乖離率の絶対値を含めて,データ・プリントを行うばあい,次のように記述する.
Y,est,y=(y3,(r-r1)/r*100)
△,pr*,y,(r-r1)/r**100,Y,abs(Y-y)/absy*100
と記述できる.
なお,変数変換($t)コマンドの直前に表示範囲指定($d)コマンドがないばあい,時系列変量は最近の100期だけ,クロスセクション変量は最初100ケースだけのプリントとなる.
- 1゜ プリント・オペランド
特定の3文字
- 「pr*」
2゜の全演算式について,各演算式のケース(期)を越える部分や,欠落値(△)についても,データ・プリントを行う.表計算への出力では,欠落値は「#N/A」と記述される.
- 「prt」
2゜の全演算式に共通にデータが存在するケース(期)についてのみ,データ・プリントを行う.欠落値(△)が1つでもあるケース(期)については,データ・プリントを行わない.
<マクロ:民間最終消費支出の百貨店販売額による回帰分析>
変量分析セクションの変量記号割当コマンドの書式($a in $$v)例1 や変数変換コマンドの書式($t in $$v)2項関数型例1 と類似のプログラムである.日本経済データセクション($$n)の時系列入力コマンド($t)で,百貨店の販売額の月次系列と,季節調整済で年率換算の名目民間最終消費支出の四半期系列を入力している.
変量分析セクション($$v)の変量記号割当($a)コマンドで,これらの系列に各1文字の変量記号x,yを割り当てている.変数変換($t)コマンドで,月次の百貨店販売額xを3ヶ月ごとに合計して4半期系列に直し,また個体識別文字系列を作成して変量記号をPとしている.そしてx変量,y変量の前年同期比増減率を求め,X変量,Y変量としている.直前に表示範囲コマンド($d)で全ケース(期間)を指示しているので,プリント「pr*」オペランドでの変量記号x,y,X,Yの数値データは全範囲が出力される.
続いて,再度の変数変換($t)コマンドの後で,X変量を基準とし,Y変量の時差を0,1,2,…と順にとる時差相関係数系列Qを作成する.次にY変量を基準とし,X変量の時差を0,1,2,…と順にとる時差相関係数系列Rを作成する.プリント「pr*」オペランドで,これらの時差相関係数系列をプリントしている.直前に表示範囲コマンド($d)による指示がないので,デフォルトの最初の100ケースまでがプリントされる.
次に回帰分析($r)コマンドの後で,X変量を説明変数,Y変量を被説明変数とする単回帰を行う.またXの2期のラグ変量を説明変数,Y変量を被説明変数とする単回帰を行い,その推定値変量をnとする.Xの2期のラグ変量と,Yの1期のラグ変量の2変量を説明変数とする重回帰によるYの推定値(外挿値を含む)変量をmとし,その重回帰の係数推定値ベクトルを求めF変量としている.民間最終消費の変化率Yを,その前期の値Yt−1と2期前の百貨店売上高変化率Xt−2から推定しようとするものであり,回帰係数ベクトルFは,3次元図上で回帰平面を描くのに用いる.観測値Y,Xと推定値n,m,残差などをプリントして回帰分析($r)を終えている.
// v-r-f1
$$n //日本経済セクション
$t //時系列入力コマンド
SDS,department sales //百貨店販売額 (MTコード88011)
CP@,consumption //民間最終消費支出(季調値,年率換算値)(MTコード100360)
$l //入力変量リスト
============ コメント行
$$v //変量分析セクション
$a //変量記号割当コマンド
x,department sales //百貨店販売額に x の変量記号
y,consumption //民間最終消費支出に y の変量記号
$d //表示範囲コマンド
all //全ケース(期間)
$t //変数変換コマンド
x=&.s(x)4,1 //[&.s]データ編集(合計)[4,1]四半期へ,1月始点
P=:ci(x) //個体識別文字列作成
X=%.c(x) //前年同期比増減率
Y=%.c(y) //前年同期比増減率
△=pr*(x,y,X,Y) //プリント
$t //変数変換コマンド
Q=crg(X,Y) //時差相関係数系列,X基準,Y時差
R=crg(Y,X) //時差相関係数系列,Y基準,X時差
△=pr*(Q,R) //プリント
------------- コメント行
$r //回帰分析コマンド
△,run,Y=(X) //単回帰の計算処理
n,est,Y=(X2) //単回帰の推定値変量
m,ext,Y=(X2,Y1) //重回帰の推定(外挿)値変量
F,@"*,Y=(X2,Y1) //重回帰の回帰係数推定値ベクトル変量
△,pr*,X,Y,n,m,Y-m //プリント
$t //変数変換コマンド
U=(X2) //Xの2期のラグ変量
V=(Y1) //Yの1期のラグ変量
================ コメント行
$$g //グラフセクション
$d //表示範囲コマンド
all //全ケース(期間)
$p //プロットコマンド
x,y //変量xと変量yを別スケールで
XY //変量X,Yを同一スケールで
Ynm //実績値と推定値n,mを同一スケールで
$p //プロットコマンド
QR //時差相関係数系列Q,R
$c //散布図コマンド
y,x,*,P //縦軸y,横軸x,回帰線*,散布点印字P
Y,X,*,P //縦軸Y,横軸X,回帰線*,散布点印字P
------------- コメント行
$3 //3次元図コマンド
Y,U,V,P,F //縦軸Y,横軸U,奥行軸V,散布点印字P,関数表示F
================== コメント行
$$ //終了セクション |
書式($r in $$v)例1のプログラム参照[v-r-f1.txt]
回帰式のプリント
回帰推定値のプロット
3次元図上の回帰平面
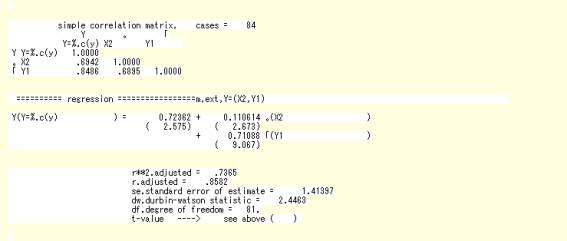
- 回帰式のプリント
 Xの2期のラグ変量と,Yの1期のラグ変量の2変量を説明変数とし,Yを被説明変数とする重回帰分析の推定結果である.民間最終消費の変化率Yを,その前期の値Yt−1と2期前の百貨店売上高変化率Xt−2で説明する回帰である.その結果は,[数値リスト]に出力される.単相関係数マトリックスの後に,回帰式の形で表示される.回帰係数推定値の下の丸括弧の中はt値である.自由度修正済決定係数,自由度修正済重相関係数,標準誤差,ダービン・ワトソン比,自由度が回帰式の下に表示される.なお,変量記号を割り当てずに演算式のまま回帰分析を行っている変数(X2やY1)は,仮想の変量記号(。や「)に置換えられて表示されている.
Xの2期のラグ変量と,Yの1期のラグ変量の2変量を説明変数とし,Yを被説明変数とする重回帰分析の推定結果である.民間最終消費の変化率Yを,その前期の値Yt−1と2期前の百貨店売上高変化率Xt−2で説明する回帰である.その結果は,[数値リスト]に出力される.単相関係数マトリックスの後に,回帰式の形で表示される.回帰係数推定値の下の丸括弧の中はt値である.自由度修正済決定係数,自由度修正済重相関係数,標準誤差,ダービン・ワトソン比,自由度が回帰式の下に表示される.なお,変量記号を割り当てずに演算式のまま回帰分析を行っている変数(X2やY1)は,仮想の変量記号(。や「)に置換えられて表示されている.
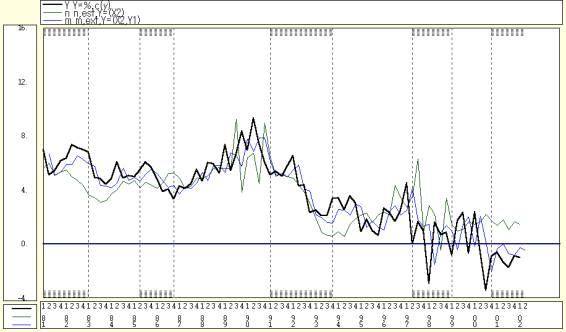
- 回帰推定値のプロット
 民間最終消費の変化率Yを,その前期の値Yt−1で説明する単回帰推定値n,前期の値Yt−1と2期前の百貨店売上高変化率Xt−2の2変数で説明する重回帰推定値mを,観測値Yとともにプロットしている.重回帰推定値mが観測値Yと同様の軌跡を描き,1期先の予測を行っていることが分かる.
民間最終消費の変化率Yを,その前期の値Yt−1で説明する単回帰推定値n,前期の値Yt−1と2期前の百貨店売上高変化率Xt−2の2変数で説明する重回帰推定値mを,観測値Yとともにプロットしている.重回帰推定値mが観測値Yと同様の軌跡を描き,1期先の予測を行っていることが分かる.
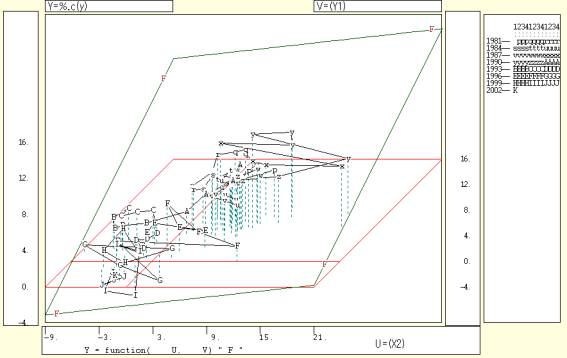
- 3次元図上の回帰平面
 縦軸に民間最終消費支出変化率Y,奥行軸にその前年の値Yt−1,横軸に2期前の百貨店販売額変化率Xt−2をとって描いた3次元図である.回帰係数ベクトルのF変量を用いて回帰平面も併せて表示している.
縦軸に民間最終消費支出変化率Y,奥行軸にその前年の値Yt−1,横軸に2期前の百貨店販売額変化率Xt−2をとって描いた3次元図である.回帰係数ベクトルのF変量を用いて回帰平面も併せて表示している.